Like Merge Sort, QuickSort is a Divide and Conquer algorithm. It picks an element as pivot and partitions the given array around the picked pivot. There are many different versions of quickSort that pick pivot in different ways.
- Always pick first element as pivot.
- Always pick last element as pivot (implemented below)
- Pick a random element as pivot.
- Pick median as pivot.
The key process in quickSort is partition(). Target of partitions is, given an array and an element x of array as pivot, put x at its correct position in sorted array and put all smaller elements (smaller than x) before x, and put all greater elements (greater than x) after x. All this should be done in linear time.
Pseudo Code for recursive QuickSort function :
/* low --> Starting index, high --> Ending index */
quickSort(arr[], low, high)
{
if (low < high)
{
/* pi is partitioning index, arr[pi] is now
at right place */
pi = partition(arr, low, high);
quickSort(arr, low, pi - 1); // Before pi
quickSort(arr, pi + 1, high); // After pi
}
}
Partition Algorithm There can be many ways to do partition, following pseudo code adopts the method given in CLRS book. The logic is simple, we start from the leftmost element and keep track of index of smaller (or equal to) elements as i. While traversing, if we find a smaller element, we swap current element with arr[i]. Otherwise we ignore current element.
/* low --> Starting index, high --> Ending index */
quickSort(arr[], low, high)
{
if (low < high)
{
/* pi is partitioning index, arr[pi] is now
at right place */
pi = partition(arr, low, high);
quickSort(arr, low, pi - 1); // Before pi
quickSort(arr, pi + 1, high); // After pi
}
}
Pseudo code for partition()
/* This function takes last element as pivot, places
the pivot element at its correct position in sorted
array, and places all smaller (smaller than pivot)
to left of pivot and all greater elements to right
of pivot */
partition (arr[], low, high)
{
// pivot (Element to be placed at right position)
pivot = arr[high];
i = (low - 1) // Index of smaller element
for (j = low; j <= high- 1; j++)
{
// If current element is smaller than the pivot
if (arr[j] < pivot)
{
i++; // increment index of smaller element
swap arr[i] and arr[j]
}
}
swap arr[i + 1] and arr[high])
return (i + 1)
}
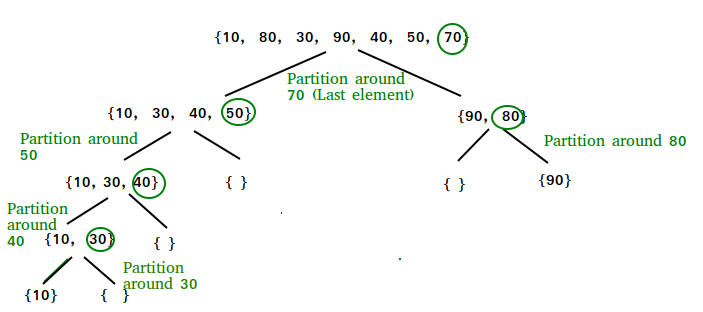
Illustration of partition() :
arr[] = {10, 80, 30, 90, 40, 50, 70}
Indexes: 0 1 2 3 4 5 6
low = 0, high = 6, pivot = arr[h] = 70
Initialize index of smaller element, i = -1
Traverse elements from j = low to high-1
j = 0 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 0
arr[] = {10, 80, 30, 90, 40, 50, 70} // No change as i and j
// are same
j = 1 : Since arr[j] > pivot, do nothing
// No change in i and arr[]
j = 2 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 1
arr[] = {10, 30, 80, 90, 40, 50, 70} // We swap 80 and 30
j = 3 : Since arr[j] > pivot, do nothing
// No change in i and arr[]
j = 4 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 2
arr[] = {10, 30, 40, 90, 80, 50, 70} // 80 and 40 Swapped
j = 5 : Since arr[j] <= pivot, do i++ and swap arr[i] with arr[j]
i = 3
arr[] = {10, 30, 40, 50, 80, 90, 70} // 90 and 50 Swapped
We come out of loop because j is now equal to high-1.
Finally we place pivot at correct position by swapping
arr[i+1] and arr[high] (or pivot)
arr[] = {10, 30, 40, 50, 70, 90, 80} // 80 and 70 Swapped
Now 70 is at its correct place. All elements smaller than
70 are before it and all elements greater than 70 are after
it.
Implementation: Following are the implementations of QuickSort:
C++
/* C++ implementation of QuickSort */
#include <bits/stdc++.h>
using namespace std;
// A utility function to swap two elements
void swap(int* a, int* b)
{
int t = *a;
*a = *b;
*b = t;
}
/* This function takes last element as pivot, places
the pivot element at its correct position in sorted
array, and places all smaller (smaller than pivot)
to left of pivot and all greater elements to right
of pivot */
int partition (int arr[], int low, int high)
{
int pivot = arr[high];// pivot
int i = (low - 1);// Index of smaller element
for (int j = low; j <= high - 1; j++)
{
// If current element is smaller than the pivot
if (arr[j] < pivot)
{
i++; // increment index of smaller element
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
/* The main function that implements QuickSort
arr[] --> Array to be sorted,
low --> Starting index,
high --> Ending index */
void quickSort( int arr[], int low, int high)
{
if (low < high)
{
/* pi is partitioning index, arr[p] is now
at right place */
int pi = partition(arr, low, high);
// Separately sort elements before
// partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
/* Function to print an array */
void printArray(int arr[], int size)
{
int i;
for (i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
// Driver Code
int main()
{
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof(arr) / sizeof(arr[0]);
quickSort(arr, 0, n - 1);
cout << "Sorted array:
";
printArray(arr, n);
return 0;
}
// This code is contributed by rathbhupendra
c
/* C implementation QuickSort */
#include<stdio.h>
// A utility function to swap two elements
void swap(int* a, int* b)
{
int t = *a;
*a = *b;
*b = t;
}
/* This function takes last element as pivot, places
the pivot element at its correct position in sorted
array, and places all smaller (smaller than pivot)
to left of pivot and all greater elements to right
of pivot */
int partition (int arr[], int low, int high)
{
int pivot = arr[high]; // pivot
int i = (low - 1); // Index of smaller element
for (int j = low; j <= high- 1; j++)
{
// If current element is smaller than the pivot
if (arr[j] < pivot)
{
i++; // increment index of smaller element
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
/* The main function that implements QuickSort
arr[] --> Array to be sorted,
low --> Starting index,
high --> Ending index */
void quickSort(int arr[], int low, int high)
{
if (low < high)
{
/* pi is partitioning index, arr[p] is now
at right place */
int pi = partition(arr, low, high);
// Separately sort elements before
// partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
/* Function to print an array */
void printArray(int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf("%d ", arr[i]);
printf("
");
}
// Driver program to test above functions
int main()
{
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof(arr)/sizeof(arr[0]);
quickSort(arr, 0, n-1);
printf("Sorted array:
");
printArray(arr, n);
return 0;
}
Java
// Java program for implementation of QuickSort
class QuickSort
{
/* This function takes last element as pivot,
places the pivot element at its correct
position in sorted array, and places all
smaller (smaller than pivot) to left of
pivot and all greater elements to right
of pivot */
int partition(int arr[], int low, int high)
{
int pivot = arr[high];
int i = (low-1); // index of smaller element
for (int j=low; j<high; j++)
{
// If current element is smaller than the pivot
if (arr[j] < pivot)
{
i++;
// swap arr[i] and arr[j]
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// swap arr[i+1] and arr[high] (or pivot)
int temp = arr[i+1];
arr[i+1] = arr[high];
arr[high] = temp;
return i+1;
}
/* The main function that implements QuickSort()
arr[] --> Array to be sorted,
low --> Starting index,
high --> Ending index */
void sort(int arr[], int low, int high)
{
if (low < high)
{
/* pi is partitioning index, arr[pi] is
now at right place */
int pi = partition(arr, low, high);
// Recursively sort elements before
// partition and after partition
sort(arr, low, pi-1);
sort(arr, pi+1, high);
}
}
/* A utility function to print array of size n */
static void printArray(int arr[])
{
int n = arr.length;
for (int i=0; i<n; ++i)
System.out.print(arr[i]+" ");
System.out.println();
}
// Driver program
public static void main(String args[])
{
int arr[] = {10, 7, 8, 9, 1, 5};
int n = arr.length;
QuickSort ob = new QuickSort();
ob.sort(arr, 0, n-1);
System.out.println("sorted array");
printArray(arr);
}
}
/*This code is contributed by Rajat Mishra */
Python
# Python program for implementation of Quicksort Sort
# This function takes last element as pivot, places
# the pivot element at its correct position in sorted
# array, and places all smaller (smaller than pivot)
# to left of pivot and all greater elements to right
# of pivot
def partition(arr,low,high):
i = ( low-1 ) # index of smaller element
pivot = arr[high] # pivot
for j in range(low , high):
# If current element is smaller than the pivot
if arr[j] < pivot:
# increment index of smaller element
i = i+1
arr[i],arr[j] = arr[j],arr[i]
arr[i+1],arr[high] = arr[high],arr[i+1]
return ( i+1 )
# The main function that implements QuickSort
# arr[] --> Array to be sorted,
# low --> Starting index,
# high --> Ending index
# Function to do Quick sort
def quickSort(arr,low,high):
if low < high:
# pi is partitioning index, arr[p] is now
# at right place
pi = partition(arr,low,high)
# Separately sort elements before
# partition and after partition
quickSort(arr, low, pi-1)
quickSort(arr, pi+1, high)
# Driver code to test above
arr = [10, 7, 8, 9, 1, 5]
n = len(arr)
quickSort(arr,0,n-1)
print ("Sorted array is:")
for i in range(n):
print ("%d" %arr[i]),
# This code is contributed by Mohit Kumra
C#
// C# program for implementation of QuickSort
using System;
class GFG {
/* This function takes last element as pivot,
places the pivot element at its correct
position in sorted array, and places all
smaller (smaller than pivot) to left of
pivot and all greater elements to right
of pivot */
static int partition(int []arr, int low,
int high)
{
int pivot = arr[high];
// index of smaller element
int i = (low - 1);
for (int j = low; j < high; j++)
{
// If current element is smaller
// than the pivot
if (arr[j] < pivot)
{
i++;
// swap arr[i] and arr[j]
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// swap arr[i+1] and arr[high] (or pivot)
int temp1 = arr[i+1];
arr[i+1] = arr[high];
arr[high] = temp1;
return i+1;
}
/* The main function that implements QuickSort()
arr[] --> Array to be sorted,
low --> Starting index,
high --> Ending index */
static void quickSort(int []arr, int low, int high)
{
if (low < high)
{
/* pi is partitioning index, arr[pi] is
now at right place */
int pi = partition(arr, low, high);
// Recursively sort elements before
// partition and after partition
quickSort(arr, low, pi-1);
quickSort(arr, pi+1, high);
}
}
// A utility function to print array of size n
static void printArray(int []arr, int n)
{
for (int i = 0; i < n; ++i)
Console.Write(arr[i] + " ");
Console.WriteLine();
}
// Driver program
public static void Main()
{
int []arr = {10, 7, 8, 9, 1, 5};
int n = arr.Length;
quickSort(arr, 0, n-1);
Console.WriteLine("sorted array ");
printArray(arr, n);
}
}
// This code is contributed by Sam007.
Output:
Sorted array:
1 5 7 8 9 10
Analysis of QuickSort Time taken by QuickSort in general can be written as following.
T(n) = T(k) + T(n-k-1) + (n)
The first two terms are for two recursive calls, the last term is for the partition process. k is the number of elements which are smaller than pivot. The time taken by QuickSort depends upon the input array and partition strategy. Following are three cases.
Worst Case: The worst case occurs when the partition process always picks greatest or smallest element as pivot. If we consider above partition strategy where last element is always picked as pivot, the worst case would occur when the array is already sorted in increasing or decreasing order. Following is recurrence for worst case.
T(n) = T(0) + T(n-1) + (n)
which is equivalent to
T(n) = T(n-1) + (n)
The solution of above recurrence is (n2).
Best Case: The best case occurs when the partition process always picks the middle element as pivot. Following is recurrence for best case.
T(n) = 2T(n/2) + (n)
The solution of above recurrence is (nLogn). It can be solved using case 2 of Master Theorem.
Average Case: To do average case analysis, we need to consider all possible permutation of array and calculate time taken by every permutation which doesn’t look easy. We can get an idea of average case by considering the case when partition puts O(n/9) elements in one set and O(9n/10) elements in other set. Following is recurrence for this case.
T(n) = T(n/9) + T(9n/10) + (n)
Solution of above recurrence is also O(nLogn)
Although the worst case time complexity of QuickSort is O(n2) which is more than many other sorting algorithms like Merge Sort and Heap Sort, QuickSort is faster in practice, because its inner loop can be efficiently implemented on most architectures, and in most real-world data. QuickSort can be implemented in different ways by changing the choice of pivot, so that the worst case rarely occurs for a given type of data. However, merge sort is generally considered better when data is huge and stored in external storage.
The end!